If you're diving into the world of CPU scheduling algorithms, the Multilevel Queue (MLQ) Scheduling Algorithm is very important concept. In real-life operating systems, processes aren’t all the same—they can be system processes, interactive tasks, or background jobs. That's where MLQ shines—it organizes processes into multiple queues based on their priority or type, each with its own scheduling strategy.
In this article, we simplify MLQ Scheduling with clear explanations and 15 solved questions to help you fully grasp the concept. Whether you're preparing for college exams, competitive tests, or just brushing up your Operating System concepts, this guide is tailored for you.
Jump To QuestionIn the Multilevel Queue Scheduling algorithm, processes are divided into multiple queues based on specific characteristics, such as priority or memory requirements. Each queue uses its own scheduling method, which could be First-Come-First-Serve (FCFS), Shortest Job First (SJF), or Round Robin (RR), depending on the types of processes it holds. This algorithm is often used in scenarios where different types of processes need to be managed separately and effectively.
- Step 1: Organize the processes into different queues based on their priority or type.
- Step 2: Choose a scheduling algorithm for each queue that meets the specific needs of the processes it contains.
- Step 3: Establish the priority levels among the queues to decide which one should be prioritized when multiple queues have processes ready to execute.
- Step 4: When a process finishes its execution in its designated queue, it is removed; if not, it may be transferred to another queue according to the system's established rules.
- Step 5: Continue repeating these steps until all processes in every queue have been completed.
| Advantages | Disadvantages |
|---|---|
| Enables specific scheduling policies for different types of processes, improving efficiency. | Static division of queues may lead to underutilization of resources if queues are imbalanced. |
| Allows easy prioritization of system processes over user processes, enhancing system performance. | Higher-priority queues can lead to starvation of processes in lower-priority queues. |
| Each queue can be customized to meet specific needs, offering flexibility. | Complex to implement and maintain, especially with a large number of queues and processes. |
| Reduces the turnaround time for certain high-priority processes. | Lack of interaction among queues can cause inefficiencies in overall CPU utilization. |
| Supports separation of long-term and short-term tasks. | Static assignment of processes means changes to process priorities are challenging. |
| Helps manage processes that require different resources effectively. | Once a process is assigned to a queue, it generally cannot be moved, reducing adaptability. |
Multilevel Queue Scheduling is especially advantageous in settings where various types of tasks need different scheduling approaches. By enabling the use of distinct scheduling algorithms for each queue and supporting priority-based processing, it can achieve better performance than a single algorithm applied to all processes. This makes it ideal for systems that need rapid responses for certain types of tasks, as well as in multiuser environments, where prioritizing system tasks can enhance stability and responsiveness.
Multilevel Queue Scheduling (MLQ) is used in computer systems
where different types of tasks need to be managed efficiently.
It's like organizing tasks into separate "queues" based on their
priority or type.
for example :
- 1. Real-Time Systems: Tasks that need immediate attention, like handling incoming video streams or medical devices, can be placed in a high-priority queue.
- 2. Interactive Systems: Tasks like typing on a keyboard or moving the mouse are placed in another queue to ensure they respond quickly.
- 3. Batch Systems: Background tasks, such as file downloads or backups, are placed in a lower-priority queue since they don’t need instant results.
By keeping tasks in separate queues, MLQ scheduling helps systems run smoothly and prioritize the most critical tasks first. It’s often used in operating systems and servers to manage resources efficiently.
Question 1 : find the average Turn Around Time and Waiting
Time of following processes using MULTILEVEL QUEUE
Scheduling (MLQ) algorithm? Consider the following processes
with their Arrival Time, Burst Time. Question criteria :
(1) There are three queue Q1, Q2, Q3
(2) In Q1 (sjf, non-preemptive), Q2(Round robin,
timestamp=2),Q3(FCFS)
| Process | Arrival Time | Burst Time | Queue name |
|---|---|---|---|
| P1 | 0 | 8 | Q2 |
| P2 | 1 | 6 | Q1 |
| P3 | 1 | 4 | Q3 |
| P4 | 2 | 3 | Q2 |
| P5 | 2 | 1 | Q1 |
| P6 | 3 | 4 | Q2 |
| P7 | 3 | 1 | Q1 |
| P8 | 4 | 2 | Q2 |
Solution:
Formula:
Turnaround Time (TAT) = Completion Time - Arrival Time
Waiting Time (WT) = Turnaround Time - Burst Time
Gantt Chart
Calculations:
| Process | Completion Time | Turnaround Time (TAT) | Waiting Time (WT) |
|---|---|---|---|
| P1 | 25 | 25 | 17 |
| P2 | 7 | 6 | 0 |
| P3 | 29 | 28 | 24 |
| P4 | 20 | 18 | 15 |
| P5 | 8 | 6 | 5 |
| P6 | 22 | 19 | 15 |
| P7 | 9 | 6 | 5 |
| P8 | 17 | 13 | 11 |
Average Turnaround Time:
(25 + 6 + 28 + 18 + 6 + 19 + 6 + 13) / 8 = 15.125
Average Waiting Time:
(17 + 0 + 24 + 15 + 5 + 15 + 5 + 11) / 8 = 11.5
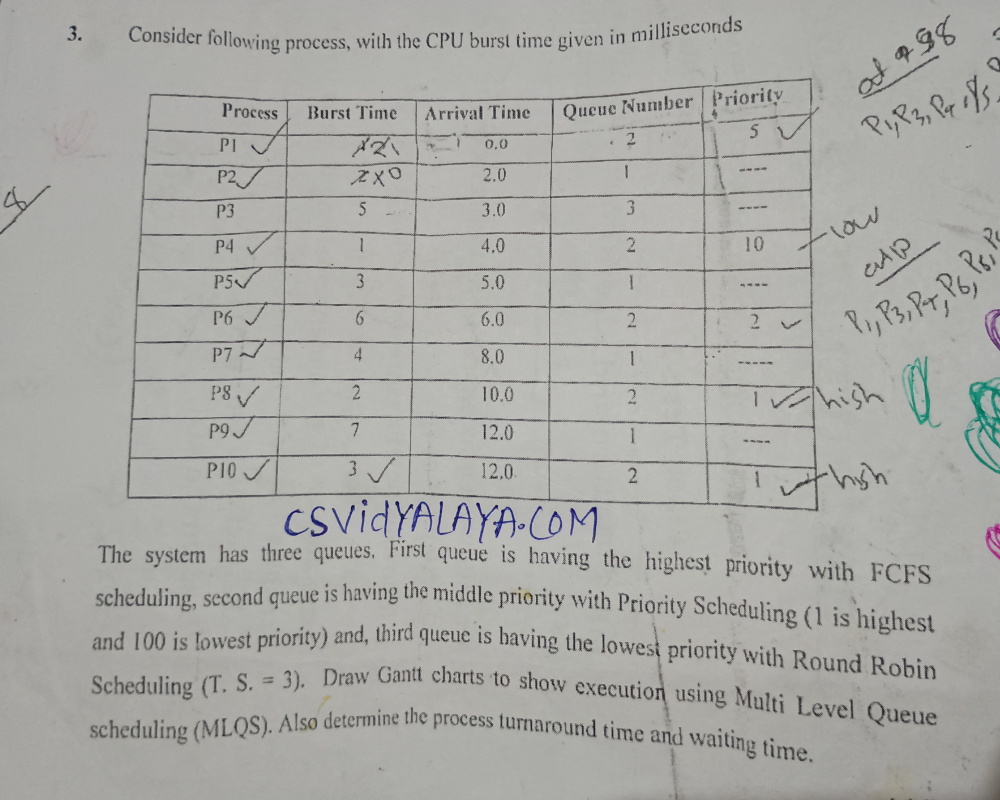
Question 2: Consider following process, with the cpu burst
time given in milliseconds.
The system has three queues, first queue is having the
highest priority with
FCFS scheduling, seconf queue is
having the middle priority with
priority scheduling (1 is highest and
100 is lowest priority) and, third queue is having the
lowest priority with
Round Robin scheduling(T.S = 3). Draw
gantt charts to show execution using Multi Level Queue
Scheduling (MLQ). Also determine the process turnAround time
and Waiting time.
| Process | Burst Time | Arrival Time | Queue name | Priority |
|---|---|---|---|---|
| P1 | 4 | 0.0 | 2 | 5 |
| P2 | 2 | 2.0 | 1 | ---- |
| P3 | 5 | 3.0 | 3 | ---- |
| P4 | 1 | 4.0 | 2 | 10 |
| P5 | 3 | 5.0 | 1 | ---- |
| P6 | 6 | 6.0 | 2 | 2 |
| P7 | 4 | 8 | 1 | ---- |
| P8 | 2 | 10.0 | 2 | 1 |
| P9 | 7 | 12.0 | 1 | ---- |
| P10 | 3 | 12.0 | 2 | 1 |
Solution:
Formula:
Turnaround Time (TAT) = Completion Time - Arrival Time
Waiting Time (WT) = Turnaround Time - Burst Time
Gantt Chart
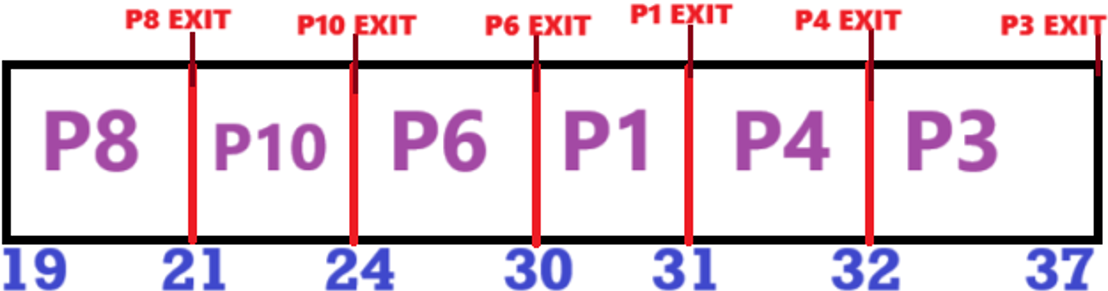
Calculations:
| Process | Completion Time | Turnaround Time (TAT) | Waiting Time (WT) |
|---|---|---|---|
| P1 | 31 | 31-0 = 31 | 31 - 4 = 27 |
| P2 | 4 | 4 - 2 = 2 | 2 - 2 = 0 |
| P3 | 37 | 37 - 3 = 34 | 34 - 5 = 29 |
| P4 | 32 | 32 - 4 = 28 | 28 - 1 = 27 |
| P5 | 8 | 8 - 5 = 3 | 3 - 3 = 0 |
| P6 | 30 | 30 - 6 = 24 | 24 - 6 = 18 |
| P7 | 12 | 12 - 8 = 4 | 4 - 4 = 0 |
| P8 | 21 | 21 - 10 = 11 | 11 - 2 = 9 |
| P9 | 19 | 19 - 12 = 7 | 7 - 7 = 0 |
| P10 | 24 | 24 - 12 = 12 | 12 - 3 = 9 |
Average Turnaround Time:
(25 + 6 + 28 + 18 + 6 + 19 + 6 + 13) / 8 = 15.125
Average Waiting Time:
(17 + 0 + 24 + 15 + 5 + 15 + 5 + 11) / 8 = 11.5
Question 3 : find the average Turn Around Time and Waiting
Time of following processes using MULTILEVEL QUEUE
Scheduling (MLQ) algorithm? Consider the following processes
with their Arrival Time, Burst Time. Question criteria :
(1) There are three queue Q1, Q2, Q3
(2) In Q1 (Priority scheduling, premptive), Q2(sjf,
preemptive) , Q3(Round robin, timestamp=1) (for priority
scheduling, take 1 is the highest priority)
| Process | Arrival Time | Burst Time | Queue Name | Priority |
|---|---|---|---|---|
| P1 | 0 | 8 | Q2 | |
| P2 | 1 | 6 | Q1 | 4 |
| P3 | 1 | 4 | Q3 | |
| P4 | 2 | 3 | Q2 | |
| P5 | 2 | 1 | Q1 | 1 |
| P6 | 3 | 4 | Q2 | |
| P7 | 3 | 1 | Q1 | 5 |
| P8 | 4 | 2 | Q2 |
Solution:
Formula:
Turnaround Time (TAT) = Completion Time - Arrival Time
Waiting Time (WT) = Turnaround Time - Burst Time
Gantt Chart
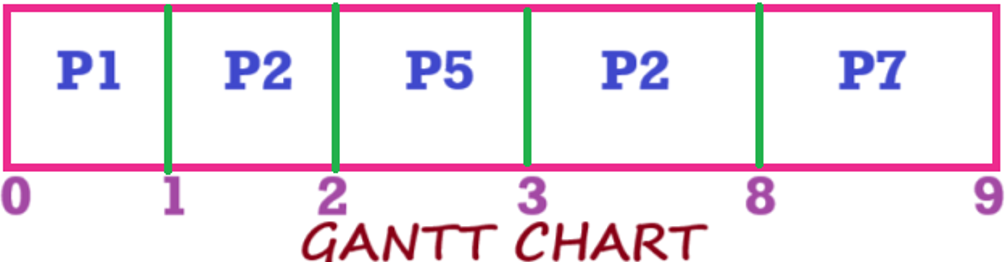
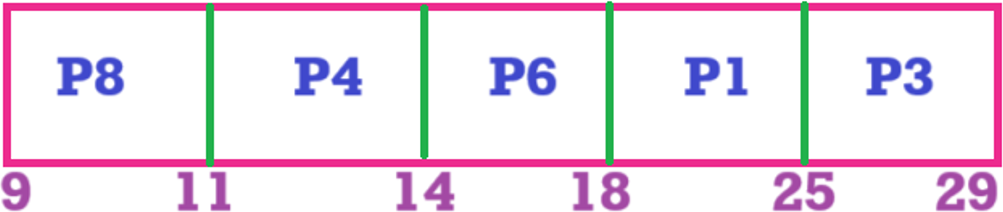
Calculations:
| Process | Completion Time | Turnaround Time (TAT) | Waiting Time (WT) |
|---|---|---|---|
| P1 | 25 | 25 | 17 |
| P2 | 8 | 7 | 1 |
| P3 | 29 | 28 | 24 |
| P4 | 14 | 12 | 9 |
| P5 | 3 | 1 | 0 |
| P6 | 18 | 15 | 11 |
| P7 | 9 | 6 | 5 |
| P8 | 11 | 7 | 5 |
Average Turnaround Time:
(25 + 7 + 28 + 12 + 1 + 15 + 6 + 7) / 8 = 12.625
Average Waiting Time:
(17 + 1 + 24 + 9 + 0 + 11 + 5 + 5) / 8 = 9
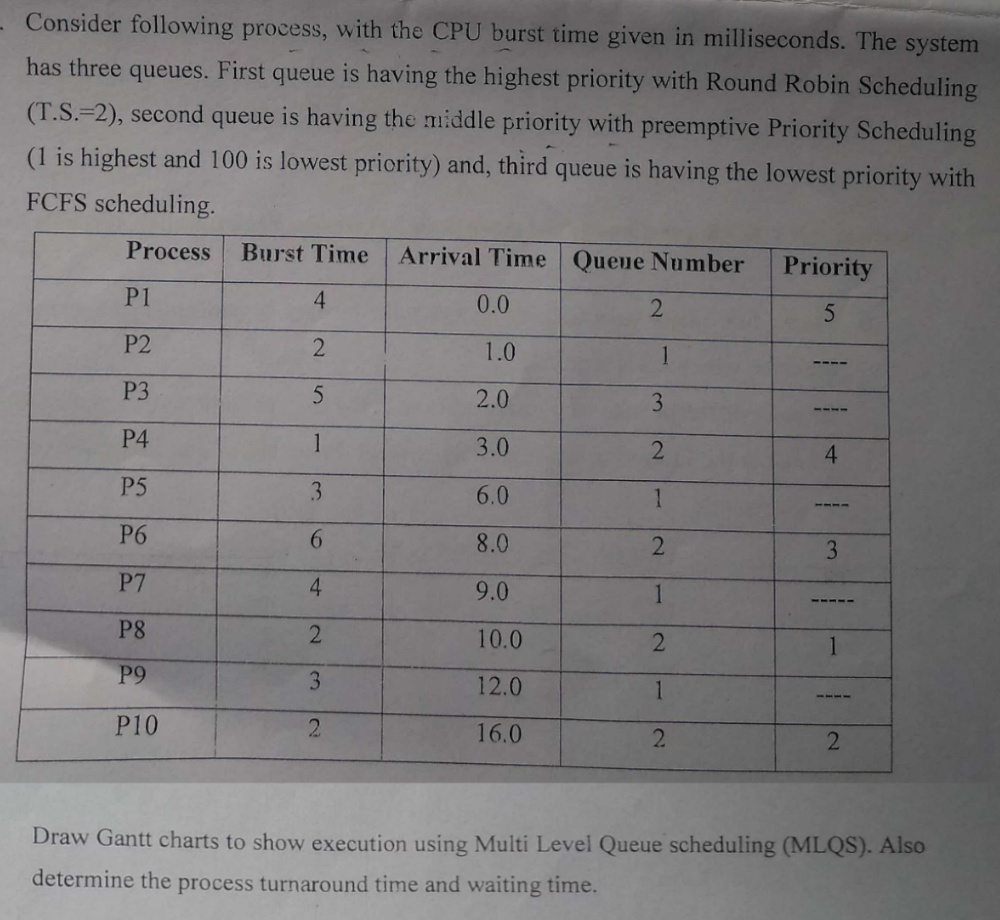
Question 4 : find the average Turn Around Time and Waiting
Time of following processes using MULTILEVEL QUEUE
Scheduling (MLQ) algorithm? Consider the following processes
with their Arrival Time, Burst Time. Question criteria :
(1) There are four queue Q1, Q2, Q3, Q4
(2) In Q1(Round robin, timestamp=1), Q2(preemptive Priority
scheduling), Q3(preemptive sjf ), Q4(FCFS) (for priority
scheduling, take 1 is the highest priority)
| Process | Arrival Time | Burst Time | Queue name | Priority |
|---|---|---|---|---|
| P1 | 0 | 6 | Q2 | 2 |
| P2 | 2 | 1 | Q1 | 1 |
| P3 | 6 | 4 | Q2 | 3 |
| P4 | 10 | 6 | Q3 | 7 |
| P5 | 18 | 12 | Q4 | 8 |
| P6 | 24 | 4 | Q1 | 10 |
| P7 | 26 | 3 | Q1 | 12 |
| P8 | 32 | 8 | Q2 | 5 |
| P9 | 36 | 6 | Q2 | 4 |
| P10 | 40 | 10 | Q3 | 6 |
Solution:
Formula:
Turnaround Time (TAT) = Completion Time - Arrival Time
Waiting Time (WT) = Turnaround Time - Burst Time
Gantt Chart
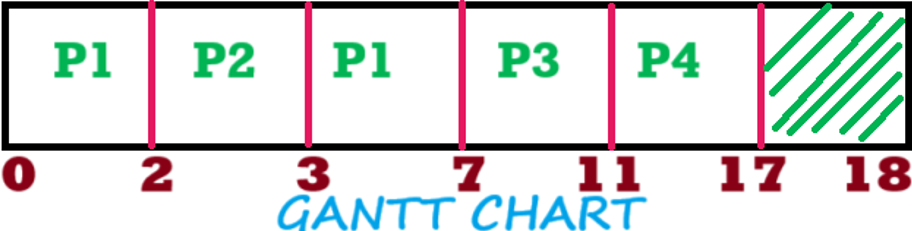
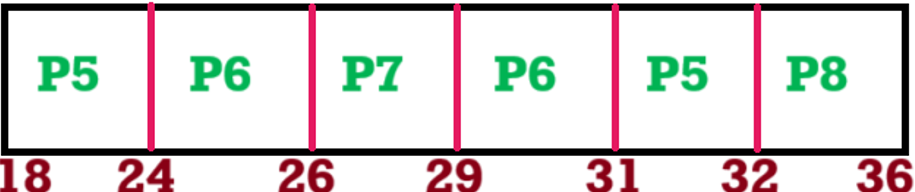
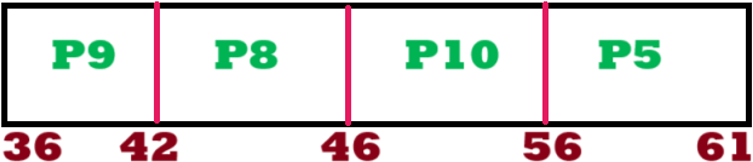
Calculations:
| Process | Completion Time | Turnaround Time (TAT) | Waiting Time (WT) |
|---|---|---|---|
| P1 | 7 | 7 | 1 |
| P2 | 3 | 1 | 0 |
| P3 | 11 | 5 | 1 |
| P4 | 17 | 7 | 1 |
| P5 | 61 | 43 | 31 |
| P6 | 31 | 7 | 3 |
| P7 | 29 | 3 | 0 |
| P8 | 46 | 14 | 6 |
| P9 | 42 | 6 | 0 |
| P10 | 56 | 16 | 6 |
Average Turnaround Time:
(7 + 1 + 5 + 7 + 43 + 7 + 3 + 14 + 6 + 16) / 10 = 10.9
Average Waiting Time:
(1 + 0 + 1 + 1 + 31 + 3 + 0 + 6 + 0 + 6) / 10 = 4.9
Previous Year Questions (PYQs) Of Multilevel Queue Scheduling (MLQ)
Below is a scanned image of a question on multilevel queue Scheduling (MLQ) in operating system